Dobrý den, je 14. 10. 2025, úterý v 42. týdnu.
Kvaternion: Porovnání verzí
(Založena nová stránka s textem „{|class="wikitable" align="right" style="text-align:center" |+Násobeni kvaternionů |- !width=15|× !width=15|1 !width=15|''i'' !width=15|''j'' !width=15|…“) |
(Žádný rozdíl)
|
Aktuální verze z 14. 5. 2016, 09:18
| × | 1 | i | j | k |
|---|---|---|---|---|
| 1 | 1 | i | j | k |
| i | i | −1 | k | −j |
| j | j | −k | −1 | i |
| k | k | j | −i | −1 |
Matematika definuje kvaterniony (latinsky "čtveřice") jak numerický systém, který rozšiřuje komplexní čísla. Poprvé je popsal irský matematik William Rowan Hamilton v roce 1843 s aplikacemi v mechanice a 3-rozměrném prostoru. Vlastností kvaternionů je, že násobení dvou kvaternionů není komutativní, tedy A x B se nerovná B x A. Hamilton definoval kvaternion jak podíl dvou přímek v 3-rozměrném prostoru nebo ekvivalentně jak podíl dvou vektorů.
Kvaterniony našly použití v teoretické i aplikované matematice, zejména pro kalkulace obsahující 3D rotace jak v 3D počítačové grafice, počítačovém vidění a v analýze krystalografických struktur. V praxi se mohou použít spolu s jinými metodami jak jsou "Eulorovy uhly" a rotační matice, nebo jak jejich alternativa, závisí na aplikaci.
V moderním matematickém jazyku, kvaterniony formují 4-rozměrní asociativní normovanou algebru s dělením nad reálními čísly, a proto i doménu ("ring theory" - teorie okruhů, abstraktní algebra). Fakticky kvaterniony tvořili první nekomutativní algebru s dělením, která byla objevena. Algebra kvaternionů se často označuje jak H (podle Hamiltona).
Algebra H má speciální místo v analýze, podle Frobeniova teorému je to jedna pouze ze dvou okruhů s dělením konečného rozměru, která obsahuje reálná čísla jak celý podokruh (proper subring), druhá je algebra komplexních čísel.
Jednotkové (normované) kvaterniony jsou přibližně jak výběr skupinové struktury na 3-sféře S3, která tvoří grupu Spin(3), která je izomorfní ke SU(2) a též ke univerzálnímu povrchu SO(3).
Obsah
Historie
Kvaternionová algebra byla uvedena Hamiltonem v roce 1843. Důležité předcházající práce byly
- Eulerova 4-čtvercová identita (1748)
- Eulerova-Rodriguesova parametrizace obecních rotací čtyřmi parametrami (1840),
ale nikdo z těchto autorů nebral 4-parametrové rotace jak algebru.
Hamilton vědel, že komplexní čísla mohou být interpretována jak geometrické body roviny a hledal způsob jak to udělat pro body 3D prostoru. Body prostoru lze reprezentovat souřednicemi, co jsou trojice čísel a po mnoho let věděl jak sčítat a odčítat trojice čísel. Ale mnoho let nevěděl jak je dělit a násobit.
Až 16.10.1843 v Dublinu během cesty do Královské irské akademie (Royal Irish Academy) přišel na vzorec
Hamilton nazval čtyřnásobek s těmito pravidly násobení "kvaternion" a věnoval zbytek svého života jejich studiu a výučbě. Klasické Hamiltonovo pojetí je víc geometrické než moderní přístup, který zdůrazňuje algebraické vlastnosti kvaternionů. Založil školu "kvaterniostů" a snažil se popularizovat kvaterniony v několika knihách. Poslední a nejdelší z jeho knih "Elementy kvaternionů" měla 800 stran.
Po smrti Hamiltona pokračoval v propagaci kvaternionů jeho student Peter Guthrie Tait. Témy ve fyzice a geometrii, které se daly vysvětlit pomocí vektorů jak kinematiky v prostoru a Maxwellovy rovnice, byly kompletně vysvětleny termíny kvaternionů.
Od poloviny 1880-tych let kvaterniony začala nahrazovat vektorová algebra, kterou vyvíjeli Josiah Willard Gibbs, Oliver Heaviside a Hermann von Helmholtz. Vektorová analýza popisoval stejné jevy jak kvaterniony, proto používá některé myšlenky a terminologii kvaternionů. Ale je konceptuálně jednodušší a přesnější na zápis, proto se role kvaternionů ve fyzice a matematice zmenšila. Boční jev toho je, že Hamiltonova práce je pro současné studenty těžko pochopitelná.
Kvaterniony se opět hodně používají od konce 20. století, primárně pro schopnost popsat prostorové rotace. Reprezentace rotací kvaterniony jsou kompaktnější a rychlejší na výpočet než použití matic. Navíc na rozdíl od Eulerových uhlů, nejsou náchylné na gimbální závěr (ztráta jednoho stupně volnosti, gimbal = Kardanův závěs). Proto se používají v počítačové grafice. Tomb Raider (1996) se často uvádí jak první populární počítačová hra, která používala kvaterniony na dosažení hladkých 3D rotací. Příklady použití kvaternionů:
- práce Nicka Bobicka Rotating Objects Using Quaternions"
- počítačové vidění
- robotika
- kontrolní teorie
- spracování signálů
- orientační kontrola
- fyzka
- bioinformatika
- molekulová dynamika
- počítačové simulace
- orbitová mechanika atd.
Například je běžné pro systémy orientační kontroly kosmické lodi, že jsou ve formě kvaternionů. Kvaterniony dostali další podporu od teorie čísel pro jejich vztah s kvadratickými formami.
Definice
Jak množina, kvaterniony H mouhou být identifikovány s R4, 4-rozměrní vektorový prostor nad reálnímí čísly. H má 3 operace:
- sčítání (addition)
- skálární násobení (scalar multiplication)
- kvaternionové násobení.
Součet dvou prvků H se definuje jak součet prvků R4. Podobně součin prvku H a reálního čísla se definuje stejně jak skalární součin v R4. Na definici součinu dvou prvků v H je nutný výběr základu (ve smyslu lineární algebry) pro R4. Elementy tohto základu se tradičně značí 1, i, j, and k. Každý element H lze jediněčně napsat jak lineární kombinaci těchto základních elementů, tedy jak Šablona:Nowrap, kde a, b, c a d jsou reální čísla. Základní element 1 bude neutrálním prvkem H, tedy násobení s 1 nic nemění a proto prvky H se obvykle píšou Šablona:Nowrap, bez základního elementu 1. Se zadaným základem, asociativní kvaternionové násobení je definováno nejprv určením součinů základních elementů a pak definicí všech dalších produktů použitím distribučního zákona.
Násobení základních elementů
Identity
- <math>i^2=j^2=k^2=ijk=-1</math>,
kde i, j a k jsou základy elementů H, určují všechny možné součiny i, j a k.
Například násobení zprav obou stran Šablona:Nowrap pomocí k dává
- <math>\begin{align}
-k & = i j k k = i j (k^2) = i j (-1), \\
k & = i j.
\end{align}</math> Všechny další možné součiny lze určit podobnými metodami, co rezultuje do
- <math>\begin{alignat}{2}
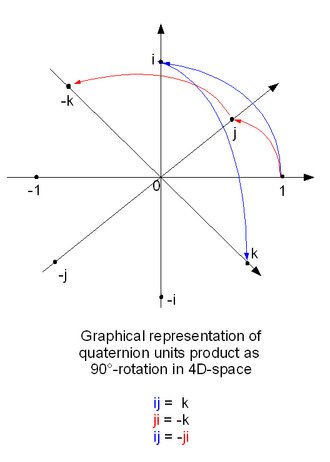
ij & = k, & \qquad ji & = -k, \\ jk & = i, & kj & = -i, \\ ki & = j, & ik & = -j, \end{alignat}</math> a to lze zapsat jak tabulku, řádky které reprezentují levý faktor součinu a sloupce reprezentují pravý faktor, jak zobrazuje obrázek v úvodu článku.
Nekomutativnost násobení
| × | 1 | i | j | k |
|---|---|---|---|---|
| 1 | 1 | i | j | k |
| i | i | −1 | k | −j |
| j | j | −k | −1 | i |
| k | k | j | −i | −1 |
Na rozdíl od násobení reálních nebo komplexních čísel, násobení kvaternionů není komutativní. Například Šablona:Nowrap, ale Šablona:Nowrap. Nekomutativita násobení má některé nečekané následky, například polynomické rovnice nad kvaterniony mohou mít víc rozdílná řešení jak stupeň polynomu. Například rovnice Šablona:Nowrap má nekonečně mnoho kvaterniových řešení Šablona:Nowrap s Šablona:Nowrap, tedy tyto řešení leží na 2-rozměrném povrchu koule centrované na nulu v 3D podprostoru kvaternionů s nulovou reální částí. Tato koule protíná komplexní rovinu v dvou bodech Šablona:Mvar a Šablona:Math.
Fakt, že násobení kvaternionů není komutativní je důvod, že kvaterniony se často používají jak příklad striktního okruhu s dělením (strictly skewed ring).
Linky a monografie
- Matrix and Quaternion FAQ v1.21 Frequently Asked Questions
- Doug Sweetser, Doing Physics with Quaternions
- Quaternions for Computer Graphics and Mechanics (Gernot Hoffman)
- The Physical Heritage of Sir W. R. Hamilton (PDF)
- D. R. Wilkins, Hamilton’s Research on Quaternions
- Quaternion Julia Fractals 3D Raytraced Quaternion Julia Fractals by David J. Grossman
- Quaternion Math and Conversions Great page explaining basic math with links to straight forward rotation conversion formulae.
- John H. Mathews, Bibliography for Quaternions.
- Quaternion powers on GameDev.net
- Andrew Hanson, Visualizing Quaternions home page.
- Charles F. F. Karney, Quaternions in molecular modeling, J. Mol. Graph. Mod. 25(5), 595–604 (January 2007); Šablona:Doi; E-print arxiv:0506177.
- Johan E. Mebius, A matrix-based proof of the quaternion representation theorem for four-dimensional rotations., arXiv General Mathematics 2005.
- Johan E. Mebius, Derivation of the Euler–Rodrigues formula for three-dimensional rotations from the general formula for four-dimensional rotations., arXiv General Mathematics 2007.
- NUI Maynooth Department of Mathematics, Hamilton Walk.
- OpenGL:Tutorials:Using Quaternions to represent rotation
- David Erickson, Defence Research and Development Canada (DRDC), Complete derivation of rotation matrix from unitary quaternion representation in DRDC TR 2005-228 paper. Drdc-rddc.gc.ca
- Alberto Martinez, University of Texas Department of History, "Negative Math, How Mathematical Rules Can Be Positively Bent",Utexas.edu
- D. Stahlke, Quaternions in Classical Mechanics Stahlke.org (PDF)
- Morier-Genoud, Sophie, and Valentin Ovsienko. "Well, Papa, can you multiply triplets?", arxiv.org describes how the quaternions can be made into a skew-commutative algebra graded by Šablona:Nowrap.
- Curious Quaternions by Helen Joyce hosted by John Baez.
- Luis Ibanez "Tutorial on Quaternions" Part I Part II (PDF; using Hamilton's terminology, which differs from the modern usage)
- R. Ghiloni, V. Moretti, A. Perotti (2013) "Continuous slice functional calculus in quaternionic Hilbert spaces," Rev.Math.Phys. 25 1350006. An expository paper about continuous functional calculus in quanternionic Hilbert spaces useful in rigorous quaternionic quantum mechanics.
Zdroj
https://en.wikipedia.org/wiki/Quaternion